自己紹介・研究目的
令和6年度修了/ ■SPRING事業 採択学生紹介

数理・ヒューマンシステム科学専攻
令和6年度 大学院入学
楊 家儒
ヨウ カジュ
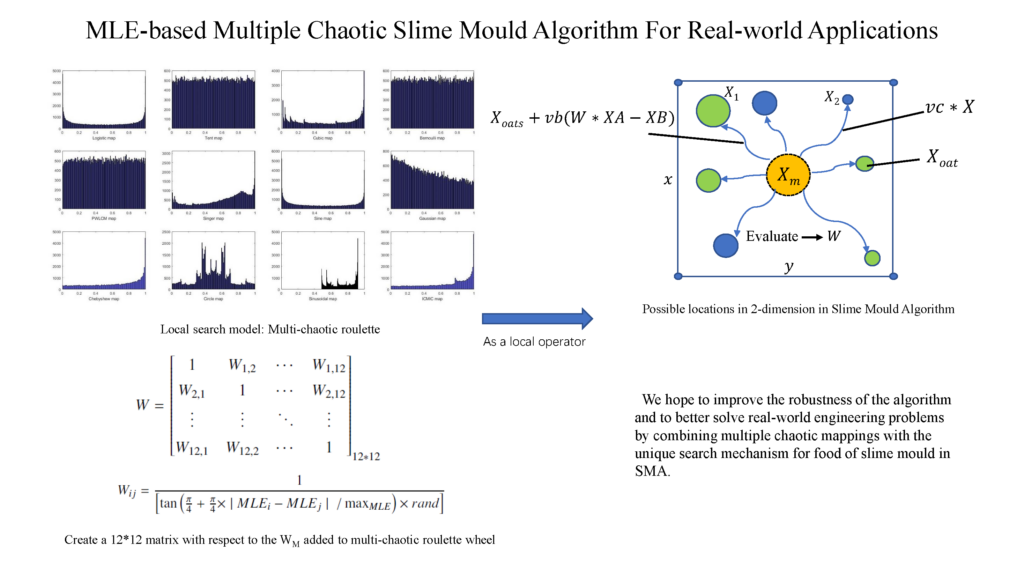
MLE-based Multiple Chaotic Slime Mould Algorithm For Real-world Applications
Hello! Everyone. My name is Jiaru Yang. I am a first-year doctor student in the department of Advanced Mathematics and Human Mechanisms of the University of Toyama. My research interests include evolutionary algorithms, machine learning, and AI security.
The goal of my study is to improve the robustness of the algorithm and to better solve real-world engineering problems by combining multiple chaotic maps with the unique search mechanism for food of slime mold in SMA, starting from the properties of chaos itself. Suitable chaotic maps are selected based on the learning probabilities of success and failure rates calculated from the success and failure memories and the analysis of the MLE values of the chaotic maps corresponding to the fitness values of the solutions. When the current chaotic map is chosen in the first iteration, we can assume that because the chaotic perturbation characteristics of that chaotic map is more in line with the current trend of the population search movement, the probability of that chaotic map and another chaotic map with the most similar MLE value is increased in the next iteration. After iteration, this mechanism selects the most suitable chaotic map for the problem at hand. Furthermore, we will explore how this technology can be adapted to existing intelligent systems to address complex practical problems. (旧フェローシップ事業採択学生)
The goal of my study is to improve the robustness of the algorithm and to better solve real-world engineering problems by combining multiple chaotic maps with the unique search mechanism for food of slime mold in SMA, starting from the properties of chaos itself. Suitable chaotic maps are selected based on the learning probabilities of success and failure rates calculated from the success and failure memories and the analysis of the MLE values of the chaotic maps corresponding to the fitness values of the solutions. When the current chaotic map is chosen in the first iteration, we can assume that because the chaotic perturbation characteristics of that chaotic map is more in line with the current trend of the population search movement, the probability of that chaotic map and another chaotic map with the most similar MLE value is increased in the next iteration. After iteration, this mechanism selects the most suitable chaotic map for the problem at hand. Furthermore, we will explore how this technology can be adapted to existing intelligent systems to address complex practical problems. (旧フェローシップ事業採択学生)